Question

Aaron took out a 30-year mortgage for $100,000 at 7%. How much will he pay over one year? (Hint: multiply the monthly mortgage payment by 12.)

Answer 1

From the statement of the problem, we know the following data of the mortgage:

• t = time = 30 years,

,

• P = principal = $100,000,

,

• r = interest rate in decimal = 7/100 = 0.07.

The monthly payments are given by the following formula:

`m=(P\cdot(r)/(12))/(1-(1+(r)/(12))^(-t\cdot12))\text{.}`

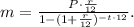
Replacing the data of the problem, we find that the monthly payments will be:

`m=(100,000\cdot(0.07)/(12))/(1-(1+(0.07)/(12))^(-30\cdot12))\cong665.302.`

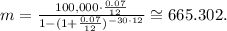
dollars.

The money that Aaron will pay in a year is 12 times the value of the monthly payment:

total of a year = 12 * $665.302 ≅ $7983.63.

Answer

Aaron will pay $7983.63 in a year.