Question

Proving that a quadrilateral with given vertices is a parallelogram

Answer 1

Given the quadrilateral PQRS

As shown the quadrilateral has the following vertices

P(-1, -7), Q(6, -4), R(2, 5), and S(-5, 2)

We will prove the quadrilateral is a parallelogram by finding the length of the sides using the following formula:

`$$d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}$$`

(a) we will find the length of PS and QR

`PS=√((-5-(-1))^2+(2-(-7)^2)=√((-4)^2+(9)^2)=√(97)`
`QR=√((2-6)^2+(5-(-4))^2)=√((-4)^2+(9)^2)=√(97)`

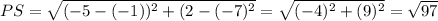
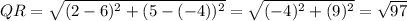
(b) we will find the slope of PS and QR

`slope\text{ }of\text{ }PS=(2--7)/(-5--1)=(9)/(-4)`
`slope\text{ }of\text{ }QR=(5--4)/(2-6)=(9)/(-4)`

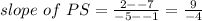
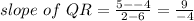
(c) From parts (a) and (b), we can conclude option 2

the quadrilateral is a parallelogram because it has one pair of opposite sides that are both congruent and parallel