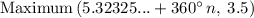Step-by-step explanation
We are given the function:
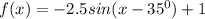
We can start with the domain and range of the function:
The function given is a sine function
Domain of a function
![\mathrm{The\:domain\:of\:a\:function\:is\:the\:set\:of\:input\:or\:argument\:values\:for\:which\:the\:function\:is\:real\:and\:defined}]()
![\begin{bmatrix}\mathrm{Solution:}\:&\:-\infty \:The range of the function[tex]\mathrm{The\:set\:of\:values\:of\:the\:dependent\:variable\:for\:which\:a\:function\:is\:defined}]()
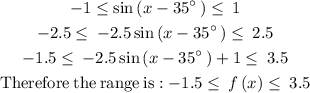
Thus, the range is
![\begin{bmatrix}\mathrm{Solution:}\:&\:-1.5\le \:f\left(x\right)\le \:3.5\:\\ \:\mathrm{Interval\:Notation:}&\:\left[-1.5,\:3.5\right]\end{bmatrix}](https://img.qammunity.org/2023/formulas/mathematics/college/s8zemkussj1wrsrto2bm4ztpqne6k0fgl2.png)
Then we can now get the maximum and minimum values
![\begin{gathered} \mathrm{Suppose\:that\:}x=c\mathrm{\:is\:a\:critical\:point\:of\:}f\left(x\right)\mathrm{\:then,\:} \\ \mathrm{If\:}f\:'\left(x\right)>0\mathrm{\:to\:the\:left\:of\:}x=c\mathrm{\:and\:}f\:'\left(x\right)<0\mathrm{\:to\:the\:right\:of\:}x=c\mathrm{\:then\:}x=c\mathrm{\:is\:a\:local\:maximum.} \\ \mathrm{If\:}f\:'\left(x\right)<0\mathrm{\:to\:the\:left\:of\:}x=c\mathrm{\:and\:}f\:'\left(x\right)>\:0\mathrm{\:to\:the\:right\:of\:}x=c\mathrm{\:then\:}x=c\mathrm{\:is\:a\:local\:minimum.} \\ \mathrm{If\:}f\:'\left(x\right)\mathrm{\:is\:the\:same\:sign\:on\:both\:sides\:of\:}x=c\mathrm{\:then\:}x=c\mathrm{\:is\:neither\:a\:local\:maximum\:nor\:a\:local\:minimum.} \end{gathered}]()
The critical points are
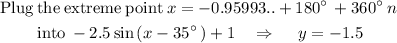
So that the minimum will be
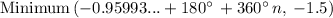
Also, the maximum is