Question

A grocer wants to mix two kinds of candy. One kind sells for $1.20 per pound, and the other sells for $2.00 per pound.He wants to mix a total of 26 pounds and sell it for $1.65 per pound. How many pounds of each kind should he use inthe new mix? (Round off the answers to the nearest hundredth.)

Answer 1

We will call the amount of each candy as X and Y.

Candy X sells for $1.20 per pound.

Candy Y sells for $2.00 per pound.

The total mix weights 26 pounds, so we can write:

`X+Y=26`

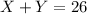
Then, the final price of the mix will be 26 pounds * 1.65 $/pound = $42.9. This final price is equal to the sum of X by its price and Y by its price:

`\begin{gathered} 1.20\cdot X+2.00\cdot Y=1.65\cdot26 \\ 1.20X+2.00Y=42.9 \end{gathered}`

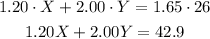
Now we have a system of equations with two unknowns.

We can replace X in the second equation knowing that:

`X=26-Y`
`\begin{gathered} 1.20\cdot(26-Y)+2Y=42.9 \\ 31.2-1.2Y+2Y=42.9 \\ -1.2Y+2Y=42.9-31.2 \\ 0.8Y=11.7 \\ Y=(11.7)/(0.8) \\ Y=14.625 \end{gathered}`

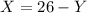
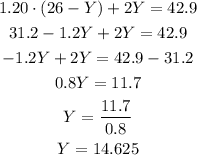
With the value of Y, we can calculate X as:

`X=26-Y=26-14.625=11.375`

Answer:

The amount of the $1.20 candy is 11.38 pounds and the amount of the $2 candy is 14.62 pounds.