Given:
angle A = 63 degrees
side b = 9
side c = 11
Asked: Find angles B and C and the length of side a.
Solution:
First, we need to find the length of side a using the cosine law.
Cosine Law:
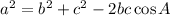
Now, let's substitute the given to the formula.
![\begin{gathered} a^2=b^2+c^2-2bc\cos A \\ a=\sqrt[]{b^2+c^2-2bc\cos A} \\ a=\sqrt[]{9^2+11^2-2\cdot11\cdot9c\cos63} \\ a=10.58819536 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/s51xl0xgzgr0890xjn4w9t9eper5uw861z.png)
Now, to find the angles B and C, we will use the sine law.
Sine Law:
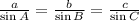
Now, let's use the value of a in the sine law. Let's get angle B first.
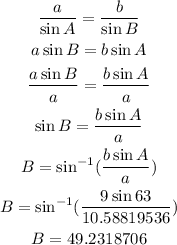
Let's repeat the process to get angle C.

Note: The sum of the internal angles of a triangle is always 180 degrees.
We can check or work if it is equal to 180 degrees, then everything is correct.
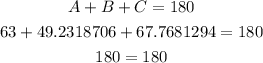
ANSWER:
length of side a = 10.6 (Rounded to the nearest tenth.)
Angle B = 49.2 degrees (Rounded to the nearest tenth.)
Angle C = 67.8 degrees (Rounded to the nearest tenth.)