Question

Function A is defined by the equation y=-2/3x+1. Which is the graph of function A?

Answer 1

We are given the equation of the following line:

`y=-(2)/(3)x+1`

This equation is of the form:

`y=mx+b`

Where "m" is the slope and "b" is the y-intercept. If the slope of a line is negative, it means that the y-values will decrease as the x-values increase, in other words, the graph will go downwards. The y-intercept indicates where the graph will touch the y-axis, in this case, that value is 1, therefore, the graph must intercept the y-axis at 1.

The options that meet these conditions are A and B. to determine which is the correct one we need to find the intercept with the x-axis, to do that we will set the value of y to zero and we'll solve for "x", like this:

`0=-(2)/(3)x+1`

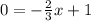
Now we subtract 1 to both sides:

`-1=-(2)/(3)x`

Now we multiply both sides by 3:

`-3=-2x`

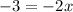
Now we divide by -2:

`\begin{gathered} (3)/(2)=x \\ 1.5=x \end{gathered}`

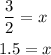
Therefore, the graph must intercept the x-axis at x = 1.5. The graph that meets all of these conditions is option A.