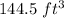Question

two containers designed to hold water are side by side, both in the shape of a cylinder. container A has a diameter of 32 feet and a height of 16 feet. container B has a diameter of 30 feet and a height of 18 feet. container A is full of water and the water is pumped into container B until container B is completely full.After the pumping is complete, what is the volume of water remaining in container A to the nearest tenth of a cubic foot?

Answer 1

Given the word problem, we can deduce the following information:

Container A:

d=32 ft

h=16 ft

Container B:

d=30 ft

h=18 ft

To determine the volume of water remaining in container A, we first get the volume of container A by using the formula:

`V=\pi((d)/(2))^2h`

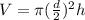
We plug in what we know:

`\begin{gathered} V=\pi((d)/(2))^(2)h \\ V=\pi((32)/(2))^2(16) \\ Calculate \\ V=12867.96\text{ }ft^3 \end{gathered}`

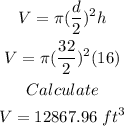
Next, we get the volume of container B using the same formula:

`\begin{gathered} V=\pi((d)/(2))^(2)h \\ V=\pi((30)/(2))^2(18) \\ Calculate \\ V=12723.45\text{ }ft^3 \end{gathered}`

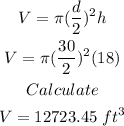
Now, we get the difference:

`\begin{gathered} Volume\text{ }Remaining=12867.96\text{ }ft^3-12723.45\text{ }ft^3 \\ Simplify \\ Volume\text{ }Remaining=144.5\text{ }ft^3 \end{gathered}`

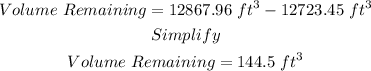
Therefore, the answer is:

`\begin{equation*} 144.5\text{ }ft^3 \end{equation*}`