We are asked to determine three consecutive even integers. Let those integers be:
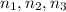
Since the integers are consecutive we have the following relationships:
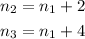
We are also given that two times the second equals the sum of the first and third. This can be expressed mathematically as:
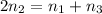
Now we can substitute the value of n3 from the previous relationship:
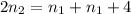
Adding like terms:
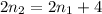
We can also substitute the value of n3:
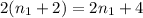
We get:
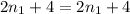
This is valid for any "n". Therefore any three consecutive integers are a solution.