We are given that the area of a rectangle is given by the following function:
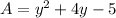
The area of a rectangle is the product of its width by its length:
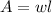
We are given that the width is:
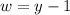
Replacing in the formula for the area we get:
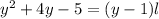
Since the area is a quadratic equation this means that for the product of the given width by the length to yield a quadratic equation the length must be of the form:
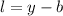
Replacing in the formula for the area:
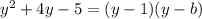
Now we need to determine the value of "b" to do that we will first solve the product on the right side.
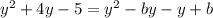
Now we subtract "y squared" from both sides:
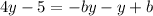
Now we associate the terms that are multiplied by "y" on the right side:
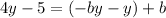
Now we take common factor on the associated terms;
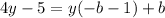
Now each coefficient for the expression on the left side and the right side must be the same, therefore we have:
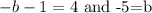
We get that b = -5. Therefore, the length of the floor must be equal to:
