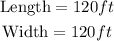Question

What is the length and width of a 480ft fence enclosed in a rectangular area

Answer 1

A rectangle is a quadrilateral having opposite sides equal

The perimeter is given by the formula

`2(L+B)`

The area is given by

`L* B`

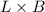
To get the maximum area

If the fence is rectangular, it will have the largest possible area when the length equals the width. In order to have a perimeter of 480 feet, that means that each side needs to be 120 feet.

For any given rectangle, the area is maximized when all the sides are equal

Thus, the maximum area is

`120ft\text{ by 120ft}`

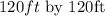
Thus, the length is

`\begin{gathered} \text{Length}=120ft \\ \text{Width}=120ft \end{gathered}`