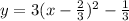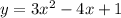
To find the vertex of a parabola (quadratic equiation) you use the next:
1. Find the axis of simetry (value of x in the vertex) with the next formula:
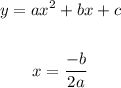
For the given equation:
b=-4
a=3
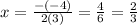
Axis of simetry x=2/3
2. Find the value of y in the vertex. Use the axis of simetry:
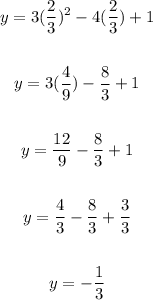
3. The vertex is (2/3 , -1/3)
4. Write in vertex form.
General vertex form of a quadratic equation:
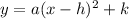
The vertex is (h,k)
For the given equation:
a=3
h=2/3
k= -1/3
Equation in vertex form: