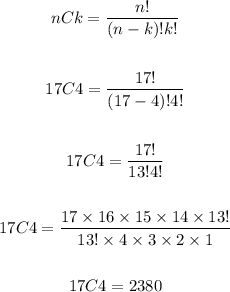Answer:
a) Number of ways to choose 4 colors from 17 if the order matters =57120
b) Number of ways to choose 4 colors from 17 if the order does not matter = 2380
Step-by-step explanation:
Total number of colors, n = 17
Number of colors to choose, k = 4
a) Number of ways to choose 4 colors from 17 if the order matters = 17P4
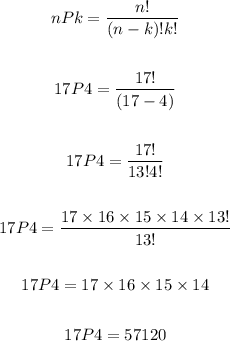
b) Number of ways to choose 4 colors from 17 if the order does not matter = 17C4