Question

A 1.4-cm tall object is 3.2 cm in front of a converging lens with a focal length of 1.8 cm. Use the mirror-thin lens equation to find the image distance and image height.

Answer 1

The image distance is 4.11 cm

The image height is 1.8 cm

Explanation:

The image distance is found by using the mirror-thin lens equation, just like this:

`(1)/(s)+(1)/(s^(\prime))=(1)/(f)`

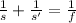
We solve and calculate for s':

`\begin{gathered} (1)/(s^(\prime))=(1)/(f)-(1)/(s) \\ (1)/(s^(\prime))=(s-f)/(f\cdot s) \\ s^(\prime)=(f\cdot s)/(s-f) \\ \text{ replacing} \\ s=3.2 \\ f=1.8 \\ s^(\prime)=(1.8\cdot3.2)/(3.2-1.8) \\ s^(\prime)=4.11 \end{gathered}`

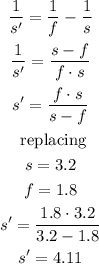
The lateral magnification of the lens is founds in terms of the object and image distances, just like this:

`\begin{gathered} M=-(s^(\prime))/(s) \\ \text{ replacing} \\ M=-(-4.11)/(3.2)=1.29 \end{gathered}`

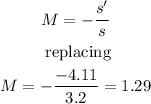
The magnitude of the lateral magnification of the lens is found in terms of the objetc and image heights:

`\begin{gathered} |M|=(h^(\prime))/(h) \\ h^(\prime)=|M|\cdot h \\ \text{ replacing} \\ h^(\prime)=1.29\cdot1.4 \\ h^(\prime)=1.8 \end{gathered}`