Question

Tammy's Coffee Shop makes a blend that is a mixture of two types of coffee. Type A coffee costs Tammy $5.35 per pound, and type B coffee costs $4.10 per pound. This month's blend used twice as many pounds of type B coffee as type A, for a total cost of $487.80. How many pounds of type A coffee were used? Number of pounds of type A coffee:

Answer 1

Given:

Type A

- cost: $5.35 per pound

Type B

-cost: $4.10 per pound

Uses twice as many pounds of type B as type A: B = 2A

Total cost - $487.80

Find: the number of pounds of Type A coffee used

Solution:

Let a = number of pounds used for Type A coffee

Let b = number of pounds used for Type B coffee

We know that the total cost for both coffee is $487.80 so, we can write equation 1:

`5.35a+4.10b=487.80`

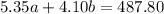
We also know that this month's blend used twice as many pounds of type B coffee as type A. This means b = 2a. So, we can replace "b" in equation 1 with "2a". So, the equation 1 becomes:

`5.35a+4.10(2a)=487.80`
`5.35a+8.2a=487.80`

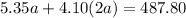
To solve for a, first, add similar terms 5.35a and 8.2a.

`13.55a=487.80`

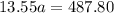
Then, divide both sides of the equation by 13.55.

`(13.55a)/(13.55)=(487.80)/(13.55)`
`a=36`

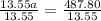
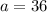
Therefore, 36 pounds of Type A coffee were used during this month.