Question

A crate rests on a flatbed truck which is initially traveling at 13.6m/s on a level road. The driver applies the brakes and the truck is brought to a halt in a distance of 41.0m. If the deceleration of the truck is constant, what is the minimum coefficient of friction between the crate and the truck that is required to keep the crate from sliding?

Answer 1

Answer:

The coefficient of friction between the crate and the truck that is required to keep the crate from sliding is 0.23

Step-by-step explanation:

The initial veocity of the truck, u = 13.6 m/s

The distance covered, s = 41.0 m

The driver applies the brakes and the truck is brought to a halt

The final velocity = 0 m/s

Calculate the deceleration by using the equation of motion below

`\begin{gathered} v^2=u^2+2as \\ 0^2=13.6^2+2a(41) \\ 82a=-13.6^2 \\ 82a=-184.96 \\ a=-(184.96)/(82) \\ a=-2.26m/s^2 \end{gathered}`

Calculate the coefficient of friction using the relationship below

`\begin{gathered} a=-\mu g \\ -2.26=-9.8\mu \\ \mu=-(2.26)/(-9.8) \\ \mu=0.23 \end{gathered}`

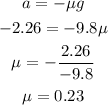
The coefficient of friction between the crate and the truck that is required to keep the crate from sliding is 0.23