Question

Find the area of the parallelogram in the figure below round your answer to the nearest 10th

Answer 1

Area of the parallelogram to the nearest 10th = 76.4 square units

Explanation:

The figure given is a parallelogram has provided by the question

Given data

The base of the parallelogram = 9

The area of the parallelogram is given below as

`\text{Area of parallelogram = base x height}`

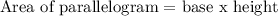
The next thing is to find the height of the parallelogram from the given below

From the above diagram, the height can be calculated using Pythagora's theorem

`\begin{gathered} \text{Pythagora's theorem is give below as} \\ (hypotenuse)^2=(opposite)^2+(adjacent)^2 \\ \text{Hypotenuse = 9} \\ \text{opposite = h} \\ \text{adjacent = 3} \\ \text{Substitute the data into the above formula} \\ 9^2=h^2+3^2 \\ 81=h^2\text{ + 9} \\ \text{Subtract 9 from both sides} \\ 81-9=h^2\text{ + 9 - 9} \\ 72=h^2 \\ \text{Take the square roots of both sides} \\ \sqrt[]{72}\text{ = }\sqrt[]{h^2} \\ h\text{ = }\sqrt[]{72} \\ h\text{ = 8.4852813742 units} \end{gathered}`

The next step after finding the height is to find the area of the parallelogram

Recall that, the area of the parallelogram = base x height

Area of the parallelogram = 9 x 8.4852813742

Area of the parallelogram = 76.3675

Area of the parallelogram to the nearest 10th = 76.4 square units