Solution
To find coterminal angles we add 2pi n
to the angle, where n is some integer, positive, negative, or zero.
Therefore when we find n, the answer will be
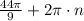
Since we want the coterminal angle to be between 0 and 2pi,
we write an inequality which indicates that:
![\begin{gathered} 0<(44\pi)/(9)+2\pi\cdot n<2\pi \\ \text{ Dividing all through by }\pi \\ \Rightarrow0<(44)/(9)+2\cdot n<2 \\ \text{ Multiply all through by }9 \\ \Rightarrow0<44+18n<18 \\ \\ \Rightarrow-44<18n<18-44 \\ \\ \Rightarrow-44<18n<-26 \\ \Rightarrow-(22)/(9)when n = -1[tex]\Rightarrow(44\pi)/(9)+2\pi\cdot n=(44\pi)/(9)-2\pi=(26)/(9)\pi]()
Hence, the value of a is 26
and the value of b is 9