Question

For f(x)=x^3+3x, determine the average rate of change of f(x) with respect to x over the interval 2≤x≤4

Answer 1

Given:

`f(x)=x^3+3x`

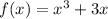
Let's determine the average rate of change with respect to x over the interval:

`2\leq x\leq4`

To find the average rate of change, apply the formula:

`avg=(f(b)-f(a))/(b-a)`

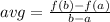
Where the closed interval is [a, b].

Thus, we have:

(a, b) ==> (2, 4)

Let's solve for f(2) and f(4).

We have:

`\begin{gathered} f(2)=2^3+3(2) \\ f(2)=8+6 \\ f(2)=14 \\ \\ \\ f(4)=4^3+3(4) \\ f(4)=64+12 \\ f(4)=76 \end{gathered}`

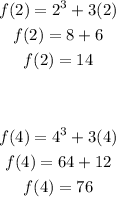
To find the average rate of change where f(a) = 14 and f(b) = 76, we have:

`\begin{gathered} \text{avg}=(f(b)-f(a))/(b-a) \\ \\ \text{avg}=(76-14)/(4-2) \\ \\ \text{avg}=(62)/(2) \\ \\ \text{avg}=31 \end{gathered}`

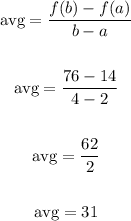
Therefore, the average rate of change of f(x) over the given interval is 31

ANSWER:

31