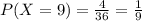Question

Let X denote the random variables that gives the sum of the faces that fall uppermost when two fair dice are rolled. Find P(X=9)

Answer 1

Consider the set of all possible outcomes when rolling two fair dice,

`S={}\lbrace(1,1),(1,2),(1,3),...,(2,1),(2,2),...,(6,4),(6,5),(6,6)\rbrace\rightarrow36\text{ possible outcomes}`

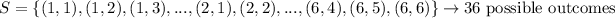
All of the combinations above are equally probable.

The combinations that give us a sum equal to 9 are,

`\begin{gathered} 3+6=6+3=9 \\ 4+5=5+4=9 \end{gathered}`

Therefore, out of the total number of combinations, only (3,6), (6,3), (4,5), and (5,4) satisfy the given condition; then,

`P(X=9)=(4)/(36)=(1)/(9)`