Question

In the diagram shown below, RQ bisects PRS. The measures of the two congruent angles are (x + 40) and (3x - 20). Solve for "x". P Р (x + 40) 0 (3x - 20° R S VI

Answer 1

Given:

Angle PRQ = (x + 40)

Angle QRS = (3x - 20)

Here, the line RQ bisects PRS. A bisector can be said to divide an angle into two equal parts.

Thus, angle PRQ = angle QRS

x + 40 = 3x - 20

Let's solve for x.

Subtract 3x from both sides:

x - 3x + 40 = 3x - 3x - 20

-2x + 40 = -20

Subtract 40 from both sides:

-2x + 40 - 40 = -20 - 40

-2x = -60

Divide both sides by -2:

`\begin{gathered} (-2x)/(-2)=(-60)/(-2) \\ \\ x\text{ = }30 \end{gathered}`

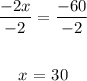
The value of x is 30

ANSWER:

x = 30