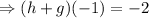Question

Suppose that the functions g and are defined for all real numbers x as follows. g(x) = 2x ^ 2; h(x) = x - 3 Write the expressions for (h - g)(x) and (hg)(x) and evaluate (h + g)(- 1) .

Answer 1

Step-by-step explanation:

The functions are given below as

`\begin{gathered} g(x)=2x^2 \\ h(x)=x-3 \end{gathered}`

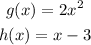
Step 1:

Find (h-g)(x)

To do this, we will use the formula below

`\begin{gathered} (h-g)(x)=h(x)-g(x) \\ (h-g)(x)=x-3-2x^2 \\ (h-g)(x)=-2x^2+x-3 \end{gathered}`

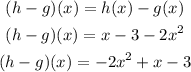
Hence,

The final answer is

`\Rightarrow(h-g)(x)=-2x^2+x-3`

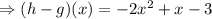
Part B:

Find (h.g)(x)

To do this, we will use the formula below

`\begin{gathered} (h.g)(x)=h(x)* g(x) \\ (h.g)(x)=(x-3)(2x^2) \\ (h.g)(x)=2x^3-6x^2 \end{gathered}`

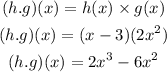
Hence,

The final answer is

`\Rightarrow(h.g)(x)=2x^3-6x^2`

Part C:

Find (h+g)(-1)

`\begin{gathered} (h+g)(x)=h(x)+g(x) \\ (h+g)(x)=2x^2+x-3 \\ (h+g)(-1)=2(-1)^2+(-1)-3 \\ (h+g)(-1)=2-1-3 \\ (h+g)(-1)=-2 \end{gathered}`

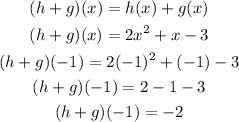
Hence,

The final answer is

`\Rightarrow(h+g)(-1)=-2`