Question

Look at the image and ask if u need anything angle 3 is the other angle in the triangle

Answer 1

The sum of the interior angles of any triangle is always 180°.

For the given right triangle:

`m\angle2+m\angle3+90=180`

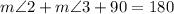
Use the given meauste for triangles 2 and 3:

`(x+8)+(2x+7)+90=180`

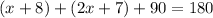
Solve the equation above for x:

`\begin{gathered} x+8+2x+7+90=180 \\ 3x+105=180 \\ \\ \text{Subtract 105 in both sides of the equation:} \\ 3x+105-105=180-105 \\ 3x=75 \\ \\ \text{Divide both sides of the equation into 3:} \\ (3)/(3)x=(75)/(3) \\ \\ x=25 \end{gathered}`

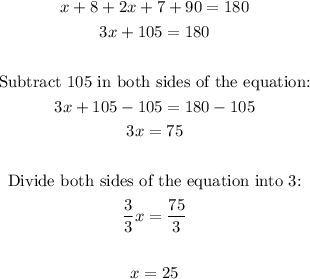
Use the value of x=25 to find the measure of angle 2:

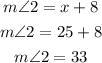
`\begin{gathered} m\angle2=x+8 \\ m\angle2=25+8 \\ m\angle2=33 \end{gathered}`Then, the measure of angle 2 is 33°