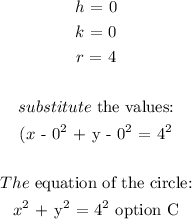Question

This circle is centered at the origin, and the length of its radius is 4. What isthe equation of the circle?55O A. (x-4)2 + (x-4)² = 16OB. +4-1O c. x² +2²=4²OD. x² +²2² = 4

Answer 1

Answer:
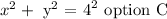
`x^2+\text{ y}^2\text{ = 4}^2\text{ \lparen option C\rparen}`Step-by-step explanation:

Given:

length of the radius = 4

Circle centered at origin

To find:

the equation of the circle

To determine the equation of the circle, we will apply the formula:

`\begin{gathered} (x\text{ - h\rparen}^2+\text{ \lparen y - k\rparen}^2\text{ = r}^2 \\ where\text{ \lparen h, k\rparen is the center of the circle} \\ r\text{ = radius} \end{gathered}`

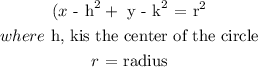
Since the circle is from the origin, the center will be (0, 0)

`\begin{gathered} h\text{ = 0} \\ k\text{ = 0} \\ r\text{ = 4} \\ \\ substitute\text{ the values:} \\ (x\text{ - 0\rparen}^2\text{ + \lparen y - 0\rparen}^2\text{ = 4}^2 \\ \\ The\text{ equation of the circle:} \\ x^2\text{ + y}^2\text{ = 4}^2\text{ \lparen option C\rparen} \end{gathered}`