Question

I need help with this problemThe last option is 0.

Answer 1

To answer this question, we need to solve the given inequality, and we can proceed as follows:

1. We have the following expression for the inequality:

`-7x+14>-3x-6`

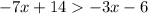
2. We need to add 3x to both sides of the inequality:

`\begin{gathered} -7x+3x+14>-3x+3x-6 \\ -7x+3x+14>-6 \\ -4x+14>-6 \end{gathered}`

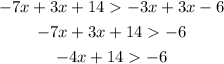
3. Now, we need to subtract 14 from both sides of the inequality as follows:

`\begin{gathered} -4x+14-14>-6-14 \\ -4x>-20 \end{gathered}`

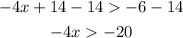
4. Finally, we need to divide both sides by -4 as follows:

`\begin{gathered} -(4)/(-4)x<-(20)/(-4) \\ x<5 \end{gathered}`

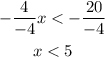
Notice that we change the direction of the inequality since we divide it by a negative number.

Therefore, the solution for the inequality is any number less than 5, or, in interval notation:

`\begin{gathered} (-\infty,5) \\ x<5 \end{gathered}`

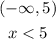
And since we have the following options, we can say that:

• -10 ---> It is part of the solution since -10 < 5.

,

• 10 ---> It is NOT part of the solution since 10 > 5.

• -5 ---> Solution ---> -5 < 5

• 5 ---> It is NOT part of the solution 5 = 5, and we need x < 5.

,

• -3 ---> Solution ---> -3 < 5

,

• 3 ---> Solution ---> 3 < 5

,

• 0 ---> Solution ---> 0 < 5

In summary, we have that the values that are solutions for the inequality are:

• -10

,

• -5

,

• -3

,

• 3

,

• 0