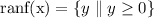Question

Graph, state the domain and range in set notation A) f(x-2)B)f (x+2)

Answer 1

We are given the graph of a quadratic function. The general form of a quadratic function is the following:

`y=a(x-h)^2+k`

Where the point:

`(h,k)`

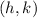
Is the vertex of the parabola. From the graph we notice that the vertex is the point (0, 0), therefore, we have:

`(h,k)=(0,0)`

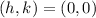
Replacing in the quadratic function we get:

`y=ax^2`

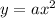
To determine the value of "a" we notice that the point:

`(x,y)=(1,1)`

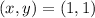
Is part of the parabola, therefore, we can substitute in the function the values x = 1 and y = 1:

`\begin{gathered} 1=a(1)^2 \\ 1=a \end{gathered}`

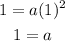
Therefore, the value of "a" is 1 and the function of the parabola is:

`y=x^2`

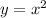
Now we are asked to determine f(x - 2).

We do this first by rewriting the equation as:

`f(x)=x^2`

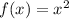
Now we will replace the value of "x" for "x - 2", we get:

`f(x-2)=(x-2)^2`

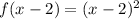
Now, to determine the graph, we need to have into account that when we subtract a number "a" to the "x" value of a function what we are doing is moving the graph "a" units to the right. Therefore, the new graph must be:

Now, to determine the domain we need to have into account that a quadratic equation is a polynomial of grade 2 and the domain of any polynomial is the real numbers, therefore, the domain is:

`\text{domf(x)}=\mleft\lbrace x\parallel x\in\R\mright\rbrace`

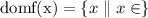
The rage in the values of the variable "y". We notice that "y" only takes positive values, therefore, the range is the real number that are greater or equal to zero, this is written as:

`\text{ranf(x)}=\mleft\lbrace y\parallel y\ge0\mright\rbrace`