b) Given the demand equation
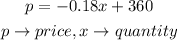
The revenue function is given by
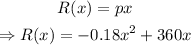
R(x) corresponds to a parabola on the plane that opens downwards; therefore, it has a maximum.
To calculate the maximum, solve the equation R'(x)=0, as shown below
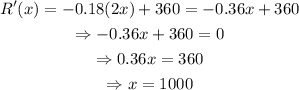
The value of x that maximizes the revenue is x=1000.
As for the maximum value of the revenue, find R(1000),
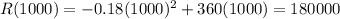
The maximum revenue is $180000
c) Find the corresponding price (p) for x=1000,
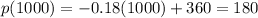
The price that maximizes revenue is $180