ANSWER
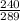
Step-by-step explanation
We want to find the value of the expression using the given figure:
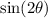
To do this, let us rewrite the expression in terms of its trigonometric identity:
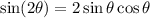
To solve this we can apply trigonometric ratios SOHCAHTOA for right triangles to find the values of sine and cosine:
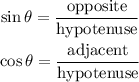
For the given triangle, we have that:
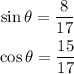
Therefore, the value of the expression is:
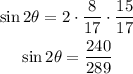
That is the answer.