A)
In order to find the function for the cost C, we can use the slope-intercept form of a linear equation:
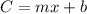
Where m is the slope and b is the y-intercept.
To calculate the value of m, we can use the formula below for the slope between two points (x1, y1) and (x2, y2):

Since x is the number of minutes and C is the cost function, we can use the ordered pairs (x, C). So, using the points (430, 150) and (880, 285), we have:
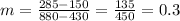
Now, to calculate the value of b, let's use the point (430, 150) in the equation (that is, x = 430 and C = 150):
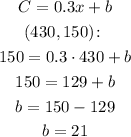
Therefore the cost function is:
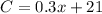
B)
Now, to find the cost for 295 minutes, let's use x = 295 and calculate the value of C:
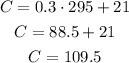
Therefore the cost for 295 minutes is $109.50.