For a function to be even, it has to meet this condition:
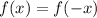
To check if the given is an even function, find f(x) and f(-x) and see if they are equal:
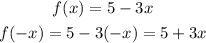
In this case, the function is not even.
For a function to be odd, it has to meet this condition:
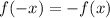
We already know that f(-x)=5+3x. Let's find -f(x):

According to this -f(x) is not equal to f(-x), which means that the function is not odd neither.
The answer is that the function is not even nor odd.