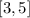Question:
Solution:
To write an equation for a line, we need a point and direction of the line. The direction is represented by the slope. Now, the slope-intercept form of a line is given by the following equation:

where m is the slope of a line and b is the y-intercept. Now, to find the slope m of this line we apply the following formula:
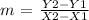
where (X1,Y1) and (X2,Y2) are points on the line. In this case, we can take the points:
(X1,Y1)= (3,4)
(X2,Y2)=(5,-7)
thus, the slope of the line KL is:
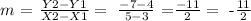
thus, the provisional equation of the line is:

now, to find b, we can take any point on the line and replace it in the above equation; then, solve for b. For example, we can take (x,y)=(3,4), thus:
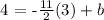
this is equivalent to:

solving for b, we get:

then
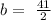
we can conclude that the slope-intercept form of the line KL is:
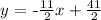
where x varies on the interval: