-2x^2+48x = 0
The expression is written in the form:
ax^2 + bx + c = 0
Where:
a = -2
b= 48
c= 0
Apply the quadratic formula:
![\frac{-b\pm\sqrt[]{b^2-4\cdot a\cdot c}}{2\cdot a}](https://img.qammunity.org/2023/formulas/mathematics/college/6ll9xrpkhophltqj6goc56svs0vp43p5j4.png)
Replacing;
![\frac{-48\pm\sqrt[]{48^2-4\cdot-2\cdot0}}{2\cdot-2}](https://img.qammunity.org/2023/formulas/mathematics/college/3168o09pqcw2mc2p0d591slrqwcbaqb418.png)
![\frac{-48\pm\sqrt[]{2304}}{-4}](https://img.qammunity.org/2023/formulas/mathematics/college/vgbphkvw23r5dmy3sqaj26vs4h2rm3cqs6.png)
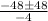
Positive;
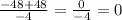
Negative:
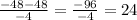
The 2 solutions are x =0 or x =24
In the context of the problem, 24 makes sense since 0 means no distance.