Question

Given the graph, description or sequence values create both an explicit and a recursive function.

Answer 1

Looking at the table, the values differ by a common ratio. This means that the values are increasing in geometric proportion. The common ratio, r is 8/4 = 16/8 = 2

The value of the first term on the table, a is 4

We can see that the next term is the product of the previous term and the common ratio

If n represents the number of terms, each consecutive term would be (n - 1) * r

Therefore, the expression for the recursive function is

`^{an-1\text{ }* r}`

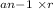
an - 1 represents the previous term

For the explicit funtion, the formula for a geometric sequence is expressed as

`\begin{gathered} Tn=ar^{n\text{ - 1}} \\ Tn=4(2)^{n\text{ - 1}} \end{gathered}`