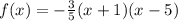Question

-Polynomial Functions-Write and solve a system of equations to find the quadratic function with the given zeros and y-intercept. Write rational coefficients as reduced fractions.

Answer 1

We We SOLUTION

Given the question in the image tab, the following are the solution steps to get the quadratic functions

Step 1: Write the zeroes and the y-intercept

`\begin{gathered} \text{roots}=\text{zeroes}=-1\text{ and 5} \\ (x,y)=(0,3),\text{ y-intercept=3} \end{gathered}`

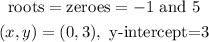
Step 2: Write the general factored form formula

`f(x)=a(x-r_1)(x-r_2)`

Step 3: Get the value of a using the zeroes and the points written in step 1

Step 4: Write the quadratic function for the system using the formula in step 2

`f(x)=-(3)/(5)(x+1)(x-5)`

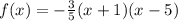
Hence, the quadratic function with the given zeroes and y-intercept in a reduced fraction form will be:

`f(x)=-(3)/(5)(x+1)(x-5)`