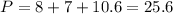Question

Find the perimeter of triangle ABC with vertices at (3,7), (3,-1), and (10,-1).Round your answer to the nearest tenth (1 decimal place!)

Answer 1

To find the perimeter of a triangle you add each of its 3 sides.

Find the measure of each side with the next formula to find the distance between two points:

`d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`

For the given triangle:

Side between (3,7) and (3,-1)

`\begin{gathered} d=\sqrt[]{(3-3)^2+(-1-7)^2} \\ \\ d=\sqrt[]{(-8)^2}=8 \end{gathered}`

Side between (3,-1) and (10,-1)

`\begin{gathered} d=\sqrt[]{(10-3)^2+(-1-(-1))^2} \\ \\ d=\sqrt[]{(7)^2}=7 \end{gathered}`

Side between (3,7) and (10,-1)

`\begin{gathered} d=\sqrt[]{(10-3)^2+(-1-7)^2} \\ \\ d=\sqrt[]{7^2+(-8)^2} \\ \\ d=\sqrt[]{49+64} \\ \\ d=\sqrt[]{113}\approx10.6 \end{gathered}`

Then, the given triangle have sides of: 8 units, 7units and 10.6 units.

Perimeter: 25.6 units
`P=8+7+10.6=25.6`