Let x be the number of napkins Carla organized in 1 hour, and y be the number of napkins Karen organized in 1 hour, then we can set the following system of equations:
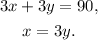
Substituting x=3y in the first equation we get:
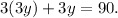
Solving for y we get:
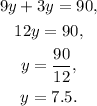
Therefore, Karen organized 7.5 napkins each hour and Carla organized 7.5x3=22.5 napkins each hour.
Answer: Since Karen organized 7.5 napkins each hour, then it would take her
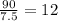
hours to do the 90 napkins.
Since Carla organized 22.5 napkins each hour, it would take her
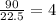
hours to do the 90 napkins.