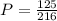Question

A fair die is rolled three times. A 1 is considered "success," while all other outcomes are "failures." Find the probability of 0 successes.The probability of 0 successes is.(Type an integer or a simplified fraction.)

Answer 1

Given that:

- A fair die is rolled three times.

- A 1 is considered "success".

- All other outcomes are "failures".

You know that a die has 6 faces numbered from 1 to 6. In this case, these outcomes are considered "failures":

`\begin{gathered} 2 \\ 3 \\ 4 \\ 5 \\ 6 \end{gathered}`

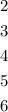
That is a total of 5 numbers considered "failures".

Since the events are independent, you can determine that the probability of 0 successes is:

`P=(5)/(6)\cdot(5)/(6)\cdot(5)/(6)`

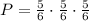
Solving the Multiplications, you get:

`P=(5\cdot5\cdot5)/(6\cdot6\cdot6)`
`P=(125)/(216)`

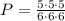
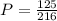
Hence, the answer is:

`P=(125)/(216)`