He bought a total of 300 pens and pencils and spend $62.50.
Each pen cost $0.25 and each pencil cost $0.15.
Lets call x the number of pens and y the number of pencils.
Then, as the sum of x and y is 300, we can write:
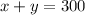
The total cost is $62.50, which is the result of adding each individual cost: the price multiplied by the quantity.
Then, we can write:
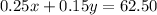
We use the information of the first equation to define y in function of x and replace in the second equation:

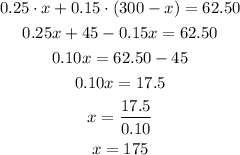
Knowing x, we can calculate y:
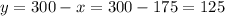
He bought 125 pencils and 175 pens.
Answer: A. 175