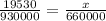Variables
• x: assessed price
,
• y: tax
Given that the tax is proportional to the assessed price, then these variables are related by the next formula:
y = kx
where k is some constant.
If we have two ordered pairs (x1, y1) and (x2, y2), the relations are:
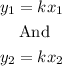
Dividing y1 by y2:

Substituting with y1 = $19,530, x1 = $930,000, x2 = $660,000, and y2 = x: