Question

Complete the squareto find the vertexof this parabola.yy? -4 2-8y-12=0([?], [ ]

Answer 1

The vertex is (-7, 4)

Step-by-step explanation

We usually see the equation of a parabola with this form:

`y=a(x-h)^2+k`

Where (h, k) is the vertex of the parabola.

But in this problem, the variables are changed, so we're looking for an equation like:

`x=b(y-k)^2+h`

The vertex is also point (h, k).

To complete the square we have to see the terms that contain y: y² - 8y

We know that a perfect square has the form:

`(a\pm b)^2=a^2\pm2ab+b^2`

If the term that contains y with exponent 1 has a coefficient 8, then we can find the second number of the binomial for the perfect square:

`(y+n)^2=y^2+2yn+\cdots=y^2-8y+\cdots`

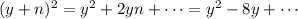
let's not think of the third term just yet. For now we have to concentrate on the second term:

`\begin{gathered} 2yn=-8y \\ 2n=-8 \\ n=-4 \end{gathered}`

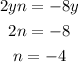
The second number for the perfect square is -4:

`(y-4)^2=y^2-8y+16`

Now we have to put this inside the equation. Since now we have a third term that is 16 we have to subtract 16 so we keep the equation true. I'll replace y²-8y by (y-4)²-16:

`-4x+(y-4)^2-16-12=0`

We can add 4x on both sides so we have the x and y separate:

`\begin{gathered} 4x=(y-4)^2-16-12 \\ 4x=(y-4)^2-28 \end{gathered}`

And finally we have to divide both sides by 4:

`x=(1)/(4)(y-4)^2-7`

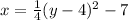
So in this case k = 4 and h = -7. The vertex is (-7, 4)