Question

-5x^2+9=0 solve quadratic equation

Answer 1

We are asked to solve the following quadratic equation:

`-5x^2+9=0`

To do that, we will solve for "x", first by subtracting 9 on both sides, like this:

`\begin{gathered} -5x^2+9-9=-9 \\ -5x^2=-9 \end{gathered}`

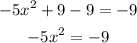
Now we will divide both sides by -5, like this:

`-(5x^2)/(-5)=-(9)/(-5)`

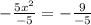
Solving the operations, we get:

`x^2=(9)/(5)`

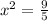
Now we take the square root on both sides of the equation, like this:

`\sqrt[]{x^2}=\sqrt[]{(9)/(5)}`

Solving the operations:

`\begin{gathered} x=\sqrt[]{(9)/(5)} \\ x=\pm\frac{3}{\sqrt[]{5}} \end{gathered}`

Since the square root has positive and negative solutions, the equation has two possible solutions, these are:

`\begin{gathered} x=\frac{3}{\sqrt[]{5}}\text{ and} \\ x=-\frac{3}{\sqrt[]{5}} \end{gathered}`