Question

Which of the following relation is an even function of x? A) |y|= x^2B) y = –2|x| C) y^2= |x| + 1 D) y = |x + 6|

Answer 1

A function is even if the graphic is symmetric with respect to the y-axis.

You can symbolize an even function as -f(x)=f(x) for all values of x on the domain of the function f.

A)

`|y|=x^2`

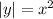
The expression |y| indicates that its the absolute value of y. This means that y can be positive or negative.

`\begin{gathered} -y=x^2 \\ and \\ y=x^2 \end{gathered}`

This function is even.

B)

`y=-2|x|`

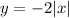
In this example x is expressed as an absolute value and can be either positive or negative:

This function is symetrical with respect to the y-axis, so it an even function.

C)

`y^2=|x|+1`
`\begin{gathered} y^2=-x+1 \\ \text{and} \\ y^2=x+1 \end{gathered}`

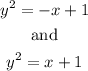
This function is not symetrical with respect to the y-axis

D)

`y=|x+6|`

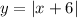
This function is not symmetrial with respect to the y-axis