Question

A pipefitter must connect two pipes as shown. The run is 32 feet while the set is 21 feet. How long a pipe will he need, and what will be the connecting angles? Round tothe nearest hundredth.

Answer 1

See below

Explanation:

Run and rise and x form a right triangle ...use pythag theorem

x^2 = 32^2 + 21^2 shows x = 38.28 ft

Right triangle tan (angle ) = opposite leg / adjacent leg

angle a = arctan ( 21/32) = 33.27° angle b = arctan (32/21) = 56.73°

Answer 2

In order to determine how long the pipe connector must be, we can use the Pythagorean Theorem.

`c^2=a^2+b^2`

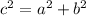
where "a" and "b" are either run or set in the diagram while "c" is the length of the pipe.

Let's say "a" is run which is 32 ft and "b" is the set which is 21 ft. Let's plug this into the formula above.

`c^2=32^2+21^2`

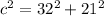
Then, solve for c.

`\begin{gathered} c^2=1024+441 \\ c^2=1465 \end{gathered}`

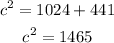
Get the square root on both sides of the equation.

`√(c^2)=√(1465)\Rightarrow c=38.275\approx38.28ft`

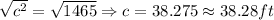
Hence, the pipe connector must be 38.28 ft.

To determine the angle, we can use either the cosine or sine functions.

For angle "a", we can use the sine function and we use the set and the length of the pipe connector.

`\theta=sin^(-1)(21)/(√(1465))`

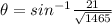
Using the calculator, the value of angle theta is:

`\theta=33.274\approx33.27\degree`

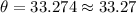
The measure of angle "a" is approximately 33.27°.

For angle "b", we can use the sine function and we use the run and the length of the pipe connector.

`\theta=sin^(-1)(32)/(√(1465))`
`\theta=56.725\approx56.73\degree`

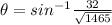
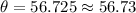
The measure of angle "b" is approximately 56.73°.