Since what we are presented with is an isosceles triangle, the missing side will be equal to the side provided by the exercise. Also, remember that the area of a rectangle is given by
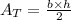
Where,
-b: the base of the triangle.
-h: the height of the triangle.
In that sense, the area of the triangle given is
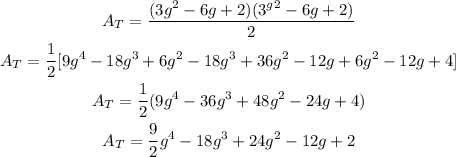
The standard form polynomial expression is given by the last equation in the above process. In other words, the answer is
9/2g^4-18g^3+24g^2-12g+2