Question

It is known that only 1% of U.S citizens living on East Coast will be exposed to Lyme disease. There is a blood test they can detect lyme disease, unfortunately, it's not a perfect taste. 95% of those exposed lenses will test positive using this blood test. 2% of those not expose a lot of these will also test positive.Given that randomly selected US citizen living on the East Coast tested positive for lyme disease, what is the probability that she has in fast been exposed to the diseaseAnswer Choices: 0.1620.3240.6480.95

Answer 1

0.324

Explanation:

From the given information:

• The probability of exposure to Lyme's disease, P(L) = 0.01

,

• The probability of testing positive given that they are exposed, P(+|L)=0.95

,

• The probability of testing positive given that they are not exposed, P(+|L')=0.02

From the first probability:

`\begin{gathered} P(L)+P(L^{^(\prime)})=1 \\ P(L^{^(\prime)})=1-P(L)=1-0.01=0.99 \end{gathered}`

We want to find the probability that given that a randomly selected person tested positive, she has in fact been exposed to the disease, P(L|+).

By the Baye's theorem for conditional probability:

`P(L|+)=(P(+|L)P(L))/(P(+|L)P(L)+P(+|L^(\prime))P(L^(\prime)))`

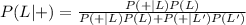
Substitute the values above:

`\begin{gathered} P(L\lvert+)=(0.95*0.01)/(0.95*0.01+0.02*0.99) \\ \approx0.324 \end{gathered}`

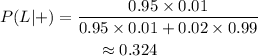
The probability is 0.324.