Question

a box with a square base and an open top must have a volume of 4000 cm^3. if the cost of the materials used is $1 per cm^2, the smallest possible cost of the box is?

Answer 1

Let

x ----> the length side of the base

h ---> is the height of the box

so

The volume of the box is given by the formula

`\begin{gathered} V=x^2h \\ V=4,000\text{ cm}^3 \\ therefore \\ 4,000=x^2h\text{ } \\ h=(4,000)/(x^2) \end{gathered}`

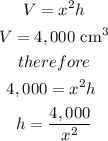
The surface area of the open box is given by the formula

`SA=x^2+4xh`

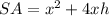
substitute the value of h in the above expression

`\begin{gathered} SA=x^2+4x(4,000)/(x^2) \\ simplify \\ SA(x)=x^2+(16,000)/(x) \end{gathered}`

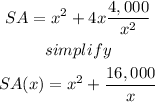
Find out the first derivative

`(dSA)/(dx)=2x-(16,000)/(x^2)`

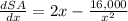
Equate to zero the first derivative, to calculate the critical point

`\begin{gathered} 2x-(16,000)/(x^2)=0 \\ \\ 2x=(16,000)/(x^2) \\ \\ x^3=8,000 \\ x=20\text{ cm} \end{gathered}`

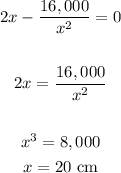
Find out the second derivative

`(d^2SA)/(dx^2)=2+(32,000)/(x^3)`

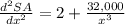
Evaluate the second derivative for x=20

The value of the second derivative for x=20 is positive

that means

The concavity is up--------> x=20 is a minimum

Find out the value of h for x=20 cm

`\begin{gathered} h=(4,000)/(x^(2)) \\ \\ h=(4,000)/(20^2) \\ h=10\text{ cm} \end{gathered}`

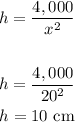
Find out the surface area for x=20 cm and h=10 cm

`\begin{gathered} SA=x^(2)+4xh \\ SA=20^2+4(20)(10) \\ SA=1,200\text{ cm}^2 \end{gathered}`

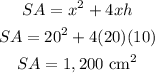
Find out the cost

Remember that

The cost of the materials used is $1 per cm^2

so

total cost=1,200(1)=$1,200

therefore

The answer is

the smallest possible cost of the box is $1,200