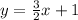Question

Write the equation of the line through the point (2,4) that is parallel to the line 3x-2y=18. Write the answer in slope-intercept form.

Answer 1

To find the equation of the line (line 1) that passes through the points (2,4) and is parallel to the line 3x - 2y = 18 (line 2), you can follow the steps above.

Step 1) Write the equation of line 2 in the slope-intercept form.

A general equation for the slope-intercept form is y = mx + b, where m is the slope and b is the y-intercept.

So, let's isolate y in line 2:

3x - 2y = 18

3y - 18 =2y

2y = 3x - 18

y = 3/2x - 18/2

y = 3/2x - 9

Step 2) Find the slope of line 1.

Since line 1 and 2 are parallel, they have the same slope.

So,

`m_1=m_2=(3)/(2)`

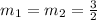
Step 3) Find the y-intercept (b) for line 1.

The equation for line 1 is

`y=(3)/(2)x+b`

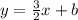
To find b, we substitute the point (2,4) in the equation:

`\begin{gathered} y=(3)/(2)x+b \\ 4=(3)/(2)\cdot2+b \\ 4=(6)/(2)+b \\ 4=3+b \\ 4-3=b \\ b=1 \end{gathered}`

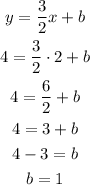
Step 4) Write the equation of the line.

Since you found m and b, you can write the equation of the line:

`y=(3)/(2)x+1`

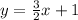
Answer:

`y=(3)/(2)x+1`