The dimensions of the rectangle are "x+7" and "x", and its area is 78in²
The area of a rectangle is equal to the product of its width and length, following the formula:
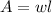
Replace it with the given dimensions of the rectangle:

To determine the dimensions of the rectangle, the first step is to determine the value of "x", to do so, you have to simplify the expression obtained above.
-First, distribute the multiplication on the parentheses term:
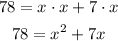
-Second, you have to equal the expression to zero. To do so, pass "78" to the right side of the equation by applying the opposite operation to both sides of it:

The expression obtained is a quadratic equation, to determine the possible values of x for this expression you have to use the quadratic formula:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
Where
a is the coefficient of the quadratic term
b is the coefficient of the x-term
c is the constant of the expression
For our equation
a=1
b=7
c=-78
Replace the values and simplify:
![\begin{gathered} x=\frac{-7\pm\sqrt[]{7^2-4\cdot1\cdot(-78)}}{2\cdot1} \\ x=\frac{-7\pm\sqrt[]{49+312}}{2} \\ x=\frac{-7\pm\sqrt[]{361}}{2} \\ x=(-7\pm19)/(2) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/7ckl9f5le5wd7zhmqi4lmecblvbgx5u2nh.png)
Next, you have to calculate the addition and subtraction separately:
-Addition:
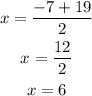
-Subtraction:
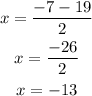
The possible values of x are 6 and -13, since there cannot be negative side lengths, the value corresponding to the rectangle's side is x=6
The final step, determine the missing side:
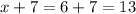
The dimensions of the rectangle are 6in and 13in