Question

The equationV=23300 (0.94)t V=23300(0.94)t represents the value (in dollars) of a car t years after its purchase.

Answer 1

The given equation is

`V=23300(0.94)^t`

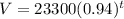
This equation represents the value of the car in dollars in t years after its purchase

Since the general form of the exponential equation is

`Y=a(1\pm r)^t`

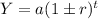
a is the initial value

r is the rate of increase (+) or decrease (-) in decimal

Compare the two equations

a = 23300

That means the purchase value of the car is $23300

Since the value in the bracket is less than 1, then use (1 - r)

1 - r = 0.94

To find r:

`\begin{gathered} 1-r=0.94 \\ 1-0.94=r \\ 0.06=r \end{gathered}`

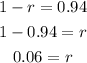
Then the rate is 0.06, change it to percent by multiplying it by 100%

`\begin{gathered} r=0.06*100\text{ \%} \\ r=6\text{ \%} \end{gathered}`

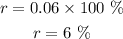
The answer is

The value of the care is V at the rate of 6%

The purchase price of the car was $23300