Question

29: If kn≠ k , and n = 1/k , which of the following expression is equivalent to (1-k)/(1-n)A. -n B. -k C. 1D. k

Answer 1

The expression if given as,

`(1-k)/(1-n)`

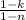
The condition is given as,

`n=(1)/(k)`

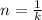
Substitute this value in the expression,

`=(1-k)/(1-(1)/(k))`

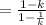
Resolve the rational expression as,

`\begin{gathered} =(1-k)/(((k-1)/(k))) \\ =(k(1-k))/(k-1) \\ =(-k(k-1))/(k-1) \end{gathered}`

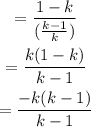
Cancelling out the common factor,

`\begin{gathered} =(-k(1))/((1)) \\ =-k \end{gathered}`

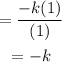
Thus, the simplified form of the given expression is obtained as,

`-k`

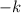
Therefore, option B is the correct choice.