Part A. We are asked to determine the derivative of each of the functions. To do that we will use the chain rule:
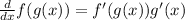
This means that we take the derivative of the function as a whole and then we multiply it by the derivative of the function inside the parenthesis.
Let's take Alice's function.
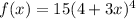
We have the following:
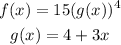
Taking the derivative of f(x) we get:
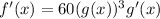
Now, we take the derivative of g(x):
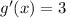
Now, we substitute the values:
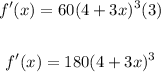
And thus we get the derivative of the function.
The same procedure is done for the other functions.
Part B.
Let's take the function for Dani's guess:
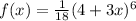
Applying the chain rule we get:
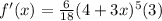
Simplifying we get:
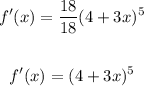
Therefore, Dani was the student that was correct.